We’re going to study particles (or projectiles) that move in two dimensions. This can be a cannon ball after being fired, a baseball after being thrown, a golf ball after being hit, a soccer ball after being kicked, or any other situation you can think of where an object is under the influence of only gravity after the initial force applied to move the object. (Usually we ignore wind resistance when we do these types of problems.)
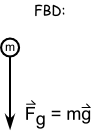The FBD of projectiles is simply a downward pointing arrow to indicate the weight. If it looks strange to have a force not in the direction of the object’s travel path, just remember that a force isn’t needed to sustain motion… it’s actually the opposite! Objects stop moving because of the forces applied to it. The FBD are always a snapshot of the forces acting on the object in that moment. The object can be moving in one direction and the force acting in another.
A projectile is a particle that is only experiencing gravity, and in most cases, gravity is only acting in one direction. Gravity doesn’t influence the horizontal motion (if we accounted for air resistance, then there would be a force in this direction as well), only the vertical motion. That’s why the ball falls to the ground when you throw it.
This means that a bullet fired horizontally from a gun experiences a constant horizontal velocity and a downward vertical acceleration. A bullet fired from a gun pointed up at a 45 degree angle also experiences a constant horizontal velocity and a downward vertical acceleration. A bullet fired from a gun in outer space away from any gravitational influences would travel up at a 45 degree path away from the gun and experience constant horizontal and vertical velocity.
Please login or register to read the rest of this content.
Thanks! It’s all making more sense, now that we’re working through the problems on the worksheets. We had fun with the easy popsicle stick launcher, too.
You can start the origin anywhere you want on the curve – in this example it’s started where the ball is first released. Imagine being on a cliff (so that the ball can dip below the horizontal). Does that help?
Yes, t = time elapsed. The half comes from when you derive the equation for acceleration from velocity (it’s more advanced math than is covered here.. for now, just assume the half is there).
When you add velocity or acceleration, they are both vectors, so you have to take into account which direction they are going in. It’s not like adding apples together… you have to take into account which direction things are moving in.
It’s also the same with forces! If you have a friend pushing your right hand and another pulling your left, that’s going to feel different than if they were both pulling you, right? That’s why you have to take direction and quantity (amount of push, in this example) into account.
In the above equations, does t stand for time elapsed?
Is the gravity subtracted because of the direction the vector is moving in?
How does 1/2 affect the acceleration and the gravity in these equations? Why do we use 1/2?
[Maybe the next lesson, on using trig with physics will help…?]
Thank you!
My student, Karis, wonders why the parabola starts where it does. Her first question upon seeing the parabolic path shown above was: Why does the projectile keep going down (below the x axis)? Can you help us understand what’s presented here? Thank you!