Two parallel lines can intersect if you are in non-Euclidean geometry. It’s hard to imagine this one being true, but it is!
If you take out a sheet of paper and draw two parallel lines, you notice that they will never cross. But what happens if you use a bigger sheet of paper? Will those longer lines ever cross? What about a sheet of paper the size of the room?
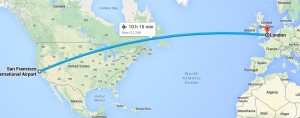
What if the paper was as large as Europe? How would you draw an airplane’s flight path between France and Switzerland? Or Ohio and India? What if the paper was the size of the Earth?
When you get to these sizes, you have to take into account the curvature of the Earth (something that regular old Euclidean geometry doesn’t do). Mapmakers have been working at this puzzle for years: trying to draw something round (the Earth, or large parts of it) on a flat sheet of paper.
Please login or register to read the rest of this content.
Not at this time, but that’s an interesting idea… I’ll put it on my list of videos to make for the website. 🙂 In the meantime, you might be interested in a set of books called “Math for Babies” where they talk about advanced topics (like calculus and non-euclidean geometry) on a really, really simple level and also on this website.
do you have anything on the website about non-Euclidean geometry?
Thanks Aurora, that was really interesting!
Laura
Sounds like it didn’t upload properly. I’ll try again. Check back in a few minutes.
Hi again Aurora,
I’ve tried to watch the video several times and it gets up to 7 seconds and then it stops itself and goes back to the beginning. I’ve tried zipping through that bit but it still doesn’t work. Please help!
Thank you
Laura